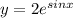Question

3. (6 Points). Solve the initial value problem y'-y.cosx=0, y(pi/2)=2e

Answer 1

`y=2e^(sin(x))`

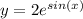
Explanation:

Given equation can be re written as

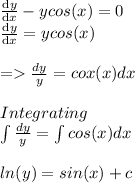`\frac{\mathrm{d} y}{\mathrm{d} x}-ycos(x)=0\\\frac{\mathrm{d} y}{\mathrm{d} x}=ycos(x)\\\\=> (dy)/(y)=cox(x)dx\\\\Integrating  \\ \int (dy)/(y)=\int cos(x)dx \\\\ln(y)=sin(x)+c`............(i)

Now it is given that y(π/2) = 2e

Applying value in (i) we get

ln(2e) = sin(π/2) + c

=> ln(2) + ln(e) = 1+c

=> ln(2) + 1 = 1 + c

=> c = ln(2)

Thus equation (i) becomes

ln(y) = sin(x) + ln(2)

ln(y) - ln(2) = sin(x)

ln(y/2) = sin(x)

`y= 2e^(sinx)`