Answer: The required solution of the given differential equation is
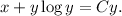
Step-by-step explanation: We are given to solve the following ordinary differential equation :

We will be using the following formulas for integration and differentiation :
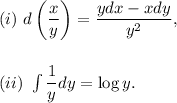
From equation (i), we have
![ydx+(y-x)dy=0\\\\\Rightarrow ydx+ydy-xdy=0\\\\\\\Rightarrow (ydx+ydy-xdy)/(y^2)=(0)/(y^2)~~~~~~~~~~~~~~~~~~~~[\textup{dividing both sides by }y^2]\\\\\\\Rightarrow (ydx-xdy)/(y^2)+(1)/(y)dy=0\\\\\\\Rightarrow d\left((x)/(y)\right)+d(\log y)=0.](https://img.qammunity.org/2020/formulas/mathematics/college/mf0904s5ii9wq682wvvczh11qjj7qwmfdi.png)
Integrating the above equation on both sides, we get
![\int d\left((x)/(y)\right)+\int d(\log y)=C~~~~~~~[\textup{where C is the constant of integration}]\\\\\\\Rightarrow (x)/(y)+\log y=C\\\\\Rightarrow x+y\log y=Cy.](https://img.qammunity.org/2020/formulas/mathematics/college/dv2g3897v9kbpegx0qtjel3opa4vrq7mem.png) .
.
Thus, the required solution of the given differential equation is
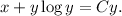 .
.