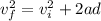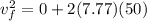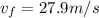Question

A 15,000 N truck starts from rest and moves down a 15∘ hill with the engine providing a 8,000 N force in the direction of the motion. Assume the rolling friction force between the truck and the road is very small. If the hill is 50 m long, what will be the speed of the truck at the bottom of the hill?

Answer 1

`v_f = 27.9 m/s`

Step-by-step explanation:

Component of the weight of the truck along the inclined plane is given as

`F_1 = W sin\theta`

`F_1 = 15000 sin15`

`F_1 = 3882.3 N`

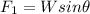
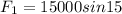
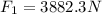
also the engine is providing the constant force to it as

`F_2 = 8000 N`

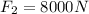
now the net force along the the plane is given as

`F_(net) = 8000 + 3882.3`

`F = 11882.3 N`

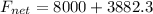
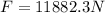
mass of the truck is given as

`m = (w)/(g) = 1529 kg`

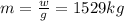
now the acceleration is given as

`a = (F)/(m)`

`a = 7.77 m/s^2`

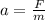
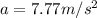
now the speed of the truck after travelling distance of d = 50 m is given as

`v_f^2 = v_i^2 + 2 a d`

`v_f^2 = 0 + 2(7.77)(50)`

`v_f = 27.9 m/s`