Answer:
A.
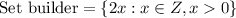
B.
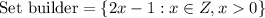
Explanation:
Set builder form is a form that defines the domain.
A.
The given arithmetic sequence is
2,4,6,8,10,.....
Here all terms are even numbers. The first term is 2 and the common difference is 2.
All the elements are multiple of 2. So, the elements are defined as 2x where x is a non zero positive integer.
The set of all 2x such that x is an integer greater than 0.
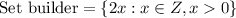
Therefore the set builder form of given elements is
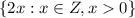 .
.
B.
The given arithmetic sequence is
1,3,5,7,....
Here all terms are odd numbers. The first term is 1 and the common difference is 2.
All the elements are 1 less than twice of an integer. So, the elements are defined as 2x-1 where x is a non zero positive integer.
The set of all 2x-1 such that x is an integer greater than 0.
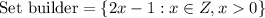
Therefore the set builder form of given elements is
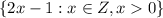 .
.