Question

Assume that you are considering the purchase of a 15-year bond with an annual coupon rate of 9.5%. The bond has face value of $1,000 and makes semiannual interest payments. If you require an 11.0% nominal yield to maturity on this investment, what is the maximum price you should be willing to pay for the bond?

Answer 1

We are going to pay $892.137 or less for the bonds.

Step-by-step explanation:

We need to calculate the present value of the bond at 11% interet rate

Cashflow from the bond:

Principal x interest = interest service

1,000 x 9.5% = 95

Present value of annuity of 95 during 15 year at 11%

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

`95 * (1-(1+.11)^(-15) )/(.11) = PV\\`

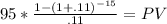
Present value of the interest service 683,1326097

Second we have to calculate the present value of the 1,000 principal in 15 years

`(Amount)/((1+rate)^(time)) ) = PV`

`(1,000)/((1+0.11)^(15)) ) = PV`

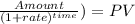
209.0043467

Finally we add both together for the present value fothe bond at our rate

209.0043467+ 683,1326097 = 892.1369564 = 892.137