Question

If a polynomial function f(x) has roots 6 and square root of 5, what must also be a root of f(x)?

A. -6
B. Square root of -5
C. 6 - Square root of 5
D. 6 + Square root of 5

Answer 1

B

Explanation:

Answer 2

-
`√(5)`

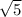
Explanation:

A root with square root or under root is only obtained when we take the square root of both sides. Remember that when we take a square root, there are two possible answers:

• One answer with positive square root
• One answer with negative square root

For example, for the equation:

`x^(2)=3`

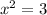
If we take the square root of both sides, the answers will be:

`x=√(3) \text{ or } x= -√(3)`

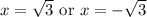
Only getting one solution with square root is not possible. Solutions with square root always occur in pairs.

For given case, the roots are 6 and
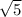`√(5)`. Therefore, the 3rd root of the polynomial function f(x) had to be -
`√(5)`

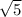
It seems you made error while writing option B, it should be - square root of 5.