I'm guessing you intended to say
 has mean
has mean
![\mu_X=E[X]=25](https://img.qammunity.org/2020/formulas/mathematics/college/1kv367luqjsn7rqwzhs591tszwux138ssh.png) and standard deviation
and standard deviation
![\sigma_x=\sqrt{\mathrm{Var}[X]}=6](https://img.qammunity.org/2020/formulas/mathematics/college/mj3sbjdspjndcuzhiwb18vasem10dsx0yl.png) , and
, and
 has means
has means
![\mu_Y=E[Y]=30](https://img.qammunity.org/2020/formulas/mathematics/college/nmbgq3wfgqeda8b22ctw6uq5jchafbjjlb.png) and standard deviation
and standard deviation
![\sigma_Y=\sqrt{\mathrm{Var}[Y]}=4](https://img.qammunity.org/2020/formulas/mathematics/college/y6za75x7xn2tesu5qe0r5q2ywdidrh6m4e.png) .
.
If
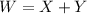 , then
, then
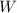 has mean
has mean
![E[W]=E[X+Y]=E[X]+E[Y]=55](https://img.qammunity.org/2020/formulas/mathematics/college/vwu3vh7zi4vhpvod555wo7he01gcxdb9iz.png)
and variance
![\mathrm{Var}[W]=E[(W-E[W])^2]=E[W^2]-E[W]^2](https://img.qammunity.org/2020/formulas/mathematics/college/1id5wr2dyqu6vrbyqow24uqi5zu6n0jpop.png)
Given that
![\mathrm{Var}[X]=36](https://img.qammunity.org/2020/formulas/mathematics/college/qxcdh9qknfr3xj4wogxzoe3jckhk1aejtu.png) and
and
![\mathrm{Var}[Y]=16](https://img.qammunity.org/2020/formulas/mathematics/college/ipuocjajujtwo7hhsul7542cv0246u6mme.png) , we have
, we have
![\mathrm{Var}[X]=E[X^2]-E[X]^2\implies E[X^2]=36+25^2=661](https://img.qammunity.org/2020/formulas/mathematics/college/m8so9m8pt6h4h2o6kwz4pjhqride5uvuxy.png)
![\mathrm{Var}[Y]=E[Y^2]-E[Y]^2\implies E[Y^2]=16+30^2=916](https://img.qammunity.org/2020/formulas/mathematics/college/zg87oasht6oxpc49aihjoi91szswr10ktr.png)
Then
![E[W^2]=E[(X+Y)^2]=E[X^2]+2E[XY]+E[Y^2]](https://img.qammunity.org/2020/formulas/mathematics/college/6zm5m7ftto5ladjqq4fdn6l024tnqcv1e7.png)
 and
and
 are independent, so
are independent, so
![E[XY]=E[X]E[Y]](https://img.qammunity.org/2020/formulas/mathematics/college/qlqcad8pc113au27tpl11hfy7u5fqiknbj.png) , and
, and
![E[W^2]=E[X^2]+2E[X]E[Y]+E[Y^2]=661+2\cdot25\cdot30+916=3077](https://img.qammunity.org/2020/formulas/mathematics/college/bwl61z9i6isjt2mw0jdjik7m85kedvmr1m.png)
so that the variance, and hence standard deviation, are
![\mathrm{Var}[W]=3077-55^2=52](https://img.qammunity.org/2020/formulas/mathematics/college/m8kwyml2b4figldrwcucczsss0nqpg73jw.png)
![\implies\sqrt{\mathrm{Var}[W]}=√(52)=\boxed{2√(13)}](https://img.qammunity.org/2020/formulas/mathematics/college/15cfbaph5lw9dx2umzo2qj0ec11rwlja3x.png)
# # #
Alternatively, if you've already learned about the variance of linear combinations of random variables, that is
![\mathrm{Var}[aX+bY]=a^2\mathrm{Var}[X]+b^2\mathrm{Var}[Y]](https://img.qammunity.org/2020/formulas/mathematics/college/5jjbew5ft6j2apiu6c5uhcilds1f15v71y.png)
then the variance of
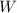 is simply the sum of the variances of
is simply the sum of the variances of
 and
and
 ,
,
![\mathrm{Var}[W]=36+16=52](https://img.qammunity.org/2020/formulas/mathematics/college/tmzurjyo1sracs7s4esn2utym2kikkms0y.png) , and so the standard deviation is again
, and so the standard deviation is again
 .
.