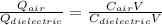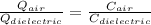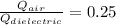Answer:
0.25
Step-by-step explanation:
A = area of each plate = 30 cm² = 30 x 10⁻⁴ m²
d = separation between the plates = 5 mm = 5 x 10⁻³ m
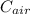 = Capacitance of capacitor when there is air between the plates
= Capacitance of capacitor when there is air between the plates
k = dielectric constant = 4
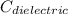 = Capacitance of capacitor when there is dielectric between the plates
= Capacitance of capacitor when there is dielectric between the plates
Capacitance of capacitor when there is air between the plates is given as
 eq-1
eq-1
Capacitance of capacitor when there is dielectric between the plates is given as
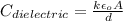 eq-2
eq-2
Dividing eq-1 by eq-2



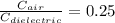
Charge stored in the capacitor when there is air is given as
 eq-3
eq-3
Charge stored in the capacitor when there is dielectric is given as
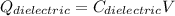 eq-4
eq-4
Dividing eq-3 by eq-4