Question

HELP

Write the explicit formula for the data.


Write a recursive rule for the height of the ball on each successive bounce.

If this ball is dropped from a height of 175 cm, how many times does it bounce before it has a bounce height of less than 8 cm? Use the same rebound percentage as in the previous problem.

What is the height of the fourth bounce of this ball if it is dropped from a height of 250 cm? Use the same rebound percentage as in the previous problem.

Answer 1

Explanation:

This is a geometric sequence so the standard formula for a recursive geometric sequence is

`a_(n)=a_(0)*r^(n-1)`

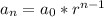
We know the heights and the number of bounces needed to achieve that height, but in order to write the recursive formula we need r.

The value of r is found by dividing each value of a bounce by the one before it. In other words, bounce 1 divided by the starting height gives a value of r=240/300 so r = .8

Bounce 2 divided by bounce 1: 192/240 = .8

So r = .8

Therefore, the formula is

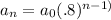`a_(n)=a_(0)(.8)^{n-1)` where

aₙ is the height of the ball after the nth bounce,

a₀ is the starting height of the ball,

.8 is the rebound percentage, and

n-1 is the number of bounces minus 1

The first problem basically asks us to find n when the starting height is 175 and the bounce height is less than 8. I used 7. Here is the formula filled in with our info:

`7=175(.8)^(n-1)`

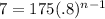
and we need to solve for n. That requires that we take the natural log of both sides. Here are the steps:

First, divide both sides by 175 to get

`.04=(.8)^(n-1)`

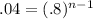
Next, take the natural log of both sides:

`ln(.04)=ln((.8)^(n-1))`

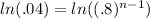
The power rule of logs says that we can bring the exponent down in front of the log:

`ln(.04)=n-1(ln(.8))`

Finding the natural logs of those decimals gives us:

`-3.218876=-.223144(n-1)`

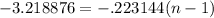
Divide both sides by -.223144 to get your n-1 value:

n - 1 = 14.4251067

That means that, since the ball is not bouncing 14.425 times, it bounces 14 times to achieve a height less than 8. Let's see how much less than 8 by checking our answer. To do this, we will solve for aₙ when x = 14:

`a_(n)=175(.8)^(14)`

This gives us a height at bounce 14 of 7.697 cm, just under 8!

Now for the next part, we want to use a starting value of 250 and .8 as the rebound height. We want to find a₄, the height of the 4th bounce.

`a_(4)=250(.8)^(4-1)`

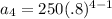
which simplifies to

`a_(4)=250(.8)^3`

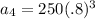
Do the math on that to find the height of the 4th bounce from a starting height of 250 cm is 128 cm

Answer 2

First case

Recursive formula:
`h_n = 0.8 * h_(n-1)`

Explicit formula:
`h_n = 300 * 0.8^(n-1)`

Second case: 15 bounces are needed

Third case: 128 cm

Explanation:

Let's call h to he height of the ball

From the table, the rate is computed as follows:

r = 240/300 = 192/240 = 153.6/192 = 122.88/153.6 = 98.3/122.88 = 0.8

Which means this is a geometric sequence (all quotients are equal).

Recursive formula:

`h_0 = 300`

`h_n = r * h_(n-1)`

`h_n = 0.8 * h_(n-1)`

where n refers to the number of bounces

Explicit formula:

`h_n = h_0 * r^(n-1)`

`h_n = 300 * 0.8^(n-1)`

If this ball is dropped from a height of 175 cm, then

`h_n = 175 * 0.8^(n-1)`

If the height must be 8 cm or less:

`8 = 175 * 0.8^(n-1)`

`8/175 = 0.8^(n-1)`

`ln(8/175) = (n-1) ln(0.8)`

`n = 1 + (ln(8/175))/(ln(0.8))`

`n = 14.83`

which means that 15 bounces are needed.

If this ball is dropped from a height of 250 cm, then

`h_n = 250 * 0.8^(n-1)`

For the fourth bounce the height will be:

`h_4 = 250 * 0.8^(4-1)`

`h_4 = 128`