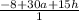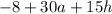Question

Let f(x)=5−8x+15x^2. Calculate the following values:

f(a)= _____


f(a+h)= ____


f(a+h)−f(a)/h= ____ for h≠0

Answer 1

`f(a)=5-8a+15a^2`

`f(a+h)=5-8a-8h+15a^2+30ah+15h^2`

`(f(a+h)-f(a))/(h)=-8+30a+15h`

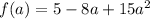
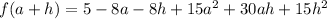
Explanation:

We are given
`f(x)=5-8x+15x^2`.

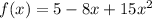We want to find
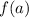`f(a)` so we just replace the x there with a giving us:

`f(a)=5-8a+15a^2`.

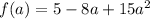We want to find
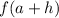`f(a+h)` so we just replace x with (a+h) now giving us:

`f(a+h)=5-8(a+h)+15(a+h)^2`.

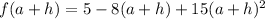We will need to distribute and multiply things out here for later use so let's go ahead and do that:

`f(a+h)=5-8(a+h)+15(a+h)^2`

`f(a+h)=5-8a-8h+15(a+h)(a+h)`

`f(a+h)=5-8a-8h+15(a^2+2ah+h^2)`

`f(a+h)=5-8a-8h+15a^2+30ah+15h^2`

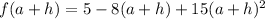
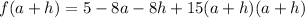
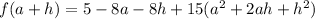
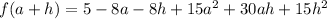
We want to find
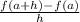`(f(a+h)-f(a))/(h)` where h is not 0.

This requires the parts we found above:

`(f(a+h)-f(a))/(h)`

`((5-8a-8h+15a^2+30ah+15h^2)-(5-8a+15a^2))/(h)`

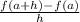
There are some thing that will zero out (cancel out) in the numerator.

You have 5-8a+15a^2 in both parenthesis and you are subtracting so that part zero's out so you have this now:

`(-8h+30ah+15h^2)/(h)`

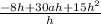
Now you can divide h from top and bottom giving you:

`(-8+30a+15h)/(1)`

`-8+30a+15h`