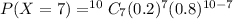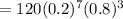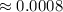Question

A quality control inspector has drawn a sample of 10 light bulbs from a recent production lot. Suppose 20% of the bulbs in the lot are defective. What is the probability that exactly 7 bulbs from the sample are defective? Round your answer to four decimal places

Answer 1

The probability is 0.0008.

Explanation:

Let X represents the event of defective bulb,

Given, the probability of defective bulb, p = 20 % = 0.2,

So, the probability that bulb is not defective, q = 1 - p = 0.8,

The number of bulbs drawn, n = 10,

Since, binomial distribution formula,

`P(x=r) = ^nC_r p^r q^(n-r)`

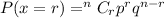
Where,
`^nC_r = (n!)/(r!(n-r)!)`

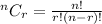
Hence, the probability that exactly 7 bulbs from the sample are defective is,

`P(X=7)=^(10)C_7 (0.2)^7 (0.8)^(10-7)`

`=120 (0.2)^7 (0.8)^3`

`=0.000786432`

`\approx 0.0008`