Question

A ball is thrown vertically upward. After t seconds, its height h (in feet) is given by the function h(t) = 52t - 16t^2 . What is the maximum height that the ball will reach?

Do not round your answer.

Answer 1

42.25 feet

Explanation:

The maximum of a quadratic can be found by finding the vertex of the parabola that the quadratic creates visually on a graph.

So first step to find the maximum height is to find the x-coordinate of the vertex.

After you find the x-coordinate of the vertex, you will want to find the y that corresponds by using the given equation,
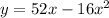`y=52x-16x^2`. The y-coordinate we will get will be the maximum height.

Let's start.

The x-coordinate of the vertex is
`(-b)/(2a)`.

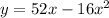`y=52x-16x^2` compare to
`y=ax^2+bx+c`.

We have that
`a=-16,b=52,c=0`.

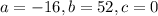Let's plug into
`(-b)/(2a)` with those values.

`(-b)/(2a)` with
`a=-16,b=52,c=0`

`(-52)/(2(-16))=(52)/(32)=(26)/(16)=(13)/(8)`.

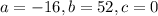
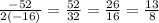The vertex's x-coordinate is 13/8.

Now to find the corresponding y-coordinate.

`y=52((13)/(8))-16((13)/(8))^2`

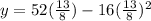
I'm going to just put this in the calculator:

`y=(169)/(4) \text{ or } 42.25`

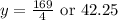
So the maximum is 42.25 feet.

Answer 2

Answer: 42.25 feet

Explanation:

We know that after "t" seconds, its height "h" in feet is given by this function:

`h(t) = 52t -16t^2`

The maximum height is the y-coordinate of the vertex of the parabola. Then, we can use the following formula to find the corresponding value of "t" (which is the x-coordinate of the vertex):

`x=t=(-b)/(2a)`

In this case:

`a=-16\\b=52`

Substituting values, we get :

`t=(-52)/(2(-16))\\\\t=1.625`

Substituting this value into the function to find the maximum height the ball will reach, we get:

`h(1.625) = 52(1.625) -16(1.625)^2\\\\h(1.625) =42.25\ ft`