Question

With only a​ part-time job and the need for a professional​ wardrobe, Rachel quickly maxed out her credit card the summer after graduation. With her first​ full-time paycheck in​ August, she vowed to pay ​$270 each month toward paying down her ​$8 comma 368 outstanding balance and not to use the card. The card has an annual interest rate of 18 percent. How long will it take Rachel to pay for her​ wardrobe? Should she shop for a new​ card? Why or why​ not?

Answer 1

In 3.5 years she will pay the wardrobe

Step-by-step explanation:

We are going to calculate the time for an annuity of 270 with monthly compound interest to achieve 8368 present value

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

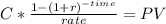
We post the know values

`270 * (1-(1+.18/12)^(-time*12) )/(.18/12) = 8,368\\`

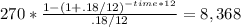
First: we clear the dividend

`1-(1+.015)^(-time*12) = 8,368* ((0.18/12))/(270)\\`

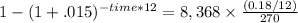
Then we set up the formula to use logarithmic

`1.015^(-time*12) = 1-.464888888888\\log_(1.015) \: 0.5351111111 = -time*12`

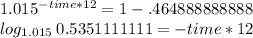
We use logarithmic properties to solve for time

`(log 0.535111111)/(log 1.015) = -41.99725593 = -42`

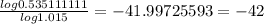
-42 = time * -12

-42/-12 = 3.5 = time

It will take 42 months or 3.5 years