Question

A product has a demand of 4000 units per year. Ordering cost is​ $20, and holding cost is​ $4 per unit per year. The​ cost-minimizing solution for this product is to​ order:? A. 200 units per order. B. all 4000 units at one time. C. every 20 days. D. 10 times per year. E. none of the above

Answer 1

A. 200 units per order

Step-by-step explanation:

To solve this you have to use the economic order quantity formula:

`Q_(opt) = \sqrt{(2DS)/(H)}`

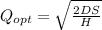
Where:

Demand = 4,000

S= supply cost = ordering cost = 20

H= holding cost = 4

`Q_(opt) = \sqrt{(2*4000*20)/(4)}`

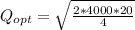
Economic Order Quantity = 200

How to Remember:

Demand per year and order cost goes in the dividend.

Holding cost goes in the divisor.