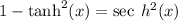Question

Prove (a) cosh2(x) − sinh2(x) = 1 and (b) 1 − tanh 2(x) = sech 2(x). SOLUTION (a) cosh2(x) − sinh2(x) = ex + e−x 2 2 − 2 = e2x + 2 + e−2x 4 − = 4 = . (b) We start with the identity proved in part (a): cosh2(x) − sinh2(x) = 1. If we divide both sides by cosh2(x), we get 1 − sinh2(x) cosh2(x) = 1 or 1 − tanh 2(x) = .

Answer 1

See explanation.

Explanation:

The hyperbolic sine and cosine functions are defined as follows:

`\sinh(x) = \frac{ {e}^(x) - {e}^( - x) }{2}`

`\cosh(x) = \frac{ {e}^(x) + {e}^( - x) }{2}`

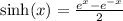
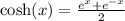
We want to show that:

`\cosh^(2) (x) - \sinh^(2) (x) = 1`

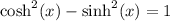
We use the definition by substituting the expressions into the left hand side and simplify to obtain the RHS.

`\cosh^(2) (x) - \sinh^(2) (x) = {( \frac{ {e}^(x) + {e}^( - x) }{2} )}^(2) + {( \frac{ {e}^(x) - {e}^( - x) }{2} )}^(2)`

`\cosh^(2) (x) - \sinh^(2) (x) = \frac{ {e}^(2x) +2 {e}^(x) {e}^( - x) + {e}^( - 2x) }{4} - \frac{ {e}^(2x) - 2 {e}^(x) {e}^( - x) + {e}^( - 2x) }{4}`

`\cosh^(2) (x) - \sinh^(2) (x) = \frac{ {e}^(2x) +2 + {e}^( - 2x) }{4} - \frac{ {e}^(2x) - 2 + {e}^( - 2x) }{4}`

`\cosh^(2) (x) - \sinh^(2) (x) = \frac{ {e}^(2x) + {e}^( - 2x) - {e}^(2x) + {e}^( - 2x )+ 2 +2 }{4}`

`\cosh^(2) (x) - \sinh^(2) (x) = ( 4 )/(4)`

`\cosh^(2) (x) - \sinh^(2) (x)=1`

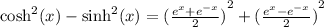
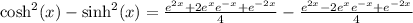
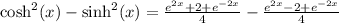
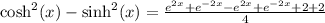
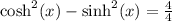
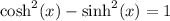
b)

If we start with the identity in a) and we divide both sides by cosh²x we get:

`(\cosh^(2) (x) )/(\cosh^(2) (x) ) -(\sinh^(2) (x) )/(\cosh^(2) (x) ) =(1)/(\cosh^(2) (x) )`

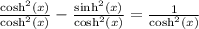
This simplifies to:

`1 - \tanh ^(2) (x) = \sec \: h ^(2) (x)`