Question

The lifetime of an alkaline battery is exponentially distributed with a mean of 20 a) What is the probability that the battery will last between 10 and 15 hours?

Answer 1

Answer: 0.1342

Explanation:

The cumulative distribution function for exponential distribution is :-

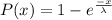`P(x)=1-e^{(-x)/(\lambda)}`, where
`\lambda` is the mean of the distribution.

Given :
`\lambda =20`

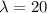
Then , the probability that the battery will last between 10 and 15 hours is given by :-

`P(10<x<15)=P(15)-P(10)\\\\=1-e^{(-15)/(20)}-(1-e^{(-10)/(20)})\\\\=-e^(-0.75)+e^(-0.5)=0.13416410697\approx0.1342`

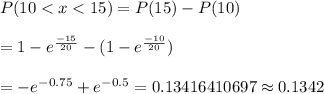
Hence, the probability that the battery will last between 10 and 15 hours = 0.1342