Answer: 6.7 g
Step-by-step explanation:
As the relative lowering of vapor pressure is directly proportional to the amount of dissolved solute.
The formula for relative lowering of vapor pressure will be,
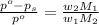
where,
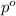 = vapor pressure of pure solvent (water) = 55.32 mmHg
= vapor pressure of pure solvent (water) = 55.32 mmHg
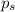 = vapor pressure of solution = 54.21 mmHg
= vapor pressure of solution = 54.21 mmHg
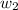 = mass of solute (urea) = ? g
= mass of solute (urea) = ? g
 = mass of solvent (water) = 100 g
= mass of solvent (water) = 100 g
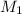 = molar mass of solvent (water) = 18 g/mole
= molar mass of solvent (water) = 18 g/mole
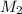 = molar mass of solute (urea) = 60 g/mole
= molar mass of solute (urea) = 60 g/mole
Now put all the given values in this formula ,we get the vapor pressure of the solution.

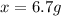
Therefore, 6.7 g of urea is needed in 100.0 g of water is needed to decrease the vapor pressure of water from 55.32 mmHg of pure water to 54.21 mmHg for the solution.