Question

Find all points (if any) of horizontal and vertical tangency to the curve. Use a graphing utility to confirm your results. (If an answer does not exist, enter DNE.) x = t2 − t + 9, y = t3 − 3t

Answer 1

The horizontal tangents occur at: (9,-2) and (11,2)

The vertical tangent occurs at (8.75,-1.375)

See attachment

Explanation:

The given parametric equations are:

`x=t^2-t+9` and
`y=t^3-3t`

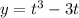
The slope function is given by:

`(dy)/(dx)=((dy)/(dt) )/((dx)/(dt) )`

`(dy)/(dx)=(3t^2-3)/(2t-1)`

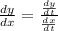
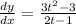
The tangent is vertical when
`(dx)/(dt)=0`

`\implies 2t-1=0`

`t=(1)/(2)`

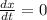
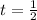
When
`t=(1)/(2)`,
`x=((1)/(2))^2-(1)/(2)+9=8.75`,
`y=0.5^3-3(0.5)=-1.375`

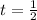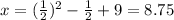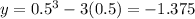
The vertical tangent occurs at (8.75,-1.375)

The tangent is horizontal when
`(dy)/(dt)=0`

`3t^2-3=0`

`\implies t=\pm1`

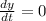
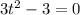
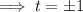
When t=1,
`x=(1)^2-1+9=9`,
`y=1^3-3(1)=-2`

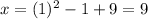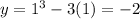
When t=-1,
`x=(-1)^2+1+9=11`,
`y=(-1)^3-3(-1)=2`

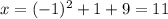The horizontal tangents occur at: (9,-2) and (11,2)