Answer: the correct option is
(D)
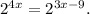
Step-by-step explanation: We are given to select the correct equation that is equivalent to the following equation :

Equivalent equations means two equations that can be obtained from one another using some properties of formula.
We will be using the following formula :
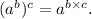
From equation (i), we have
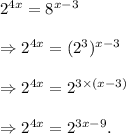
Thus, the required equivalent equation is
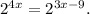
Option (D) is CORRECT.