Question

A print shop purchases a new printer for $25,000. The equipment depreciates at a rate of 5% each year. The relationship between the value of the printer, y, and the year number, x, can be represented by the equation, y = 25,000 • 0.95 x . Complete the table below with the value of the printer, to the nearest cent, in years 1, 2, and 3. Include proper commas and decimals in your answer.

Answer 1

Part 1) For x=1 year,
`y=\$23,750`

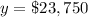
Part 2) For x=2 years,
`y=\$22,562.50`

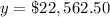
Part 3) For x=3 years,
`y=\$21,434.38`

Explanation:

we know that

The formula to calculate the depreciated value is equal to

`y=P(1-r)^(x)`

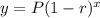
where

y is the depreciated value

P is the original value

r is the rate of depreciation in decimal

x is the number of years

in this problem we have

`P=\$25,000\\r=5\%=0.05`

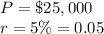
substitute

`y=25,000(1-0.05)^(x)`

`y=25,000(0.95)^(x)`

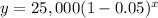
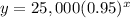
Part 1) Find the value of the printer, to the nearest cent, in year 1

so

For x=1 year

substitute in the exponential equation

`y=25,000(0.95)^(1)`

`y=\$23,750`

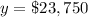
Part 2) Find the value of the printer, to the nearest cent, in year 2

so

For x=2 years

substitute in the exponential equation

`y=25,000(0.95)^(2)`

`y=\$22,562.50`

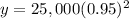
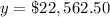
Part 3) Find the value of the printer, to the nearest cent, in year 3

so

For x=3 years

substitute in the exponential equation

`y=25,000(0.95)^(3)`

`y=\$21,434.38`