Question

The Office of Student Services at a large western state university maintains information on the study habits of its full-time students. Their studies indicate that the mean amount of time undergraduate students study per week is 20 hours. The hours studied follows the normal distribution with a standard deviation of six hours. Suppose we select a random sample of 144 current students. What is the probability that the mean of this sample is between 19.25 hours and 21.0 hours?

(A) 0.4332
(B) 0.8664
(C) 0.9104
(D) 0.0181

Answer 1

Answer: (C) 0.9104

Explanation:

Given : The hours studied follows the normal distribution

Mean :
`\mu=\text{20 hours}`

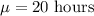
Standard deviation :
`\sigma=6\text{ hours}`

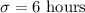
Sample size :
`n=144`

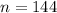
The formula to calculate the z-score is given by :-

`z=(x-\mu)/((\sigma)/(√(n)))`

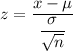
Let x be the number hours taken by randomly selected undergraduated student.

Then for x = 19.25 , we have

`z=(19.25-20)/((6)/(√(144)))=-1.5`

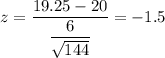
for x = 21.0 , we have

`z=(20-21)/((6)/(√(144)))=2`

The p-value :
`P(19.25<x<21)=P(-1.5<z<2)`

`P(2)-P(-1.5)= 0.9772498- 0.0668072=0.9104426\approx0.9104`

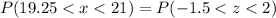
Thus, the probability that the mean of this sample is between 19.25 hours and 21.0 hours = 0.9104.