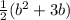Answer:
A(b) =
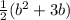
Explanation:
Given: Height of the triangle is 3 units more than the base.
Let "b" be the base of the triangle.
So, h = b + 3
Area of a triangle A =
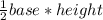
Now plug in h = b +3 in the above area of formula, we get
A(b) =
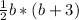
Now we can multiply b and (b + 3), we get
A(b) =
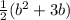
Therefore, the answer is A(b) =