Question

Let sin t = a​, cos t = b​, and tan t = c. Write the expression in terms of​ a, b, and c.

-sin(-t - 8 π) + cos(-t - 2 π) + tan(-t - 5 π)

Answer 1

`a+b-c`

*Note c could be written as a/b

Explanation:

-sin(-t - 8 π) + cos(-t - 2 π) + tan(-t - 5 π)

The identities I'm about to apply:

`\sin(a-b)=\sin(a)\cos(b)-\sin(b)\cos(a)`

`\cos(a-b)=\cos(a)\cos(b)+\sin(a)\sin(b)`

`\tan(a-b)=(\tan(a)-\tan(b))/(1+\tan(a)\tan(b))`

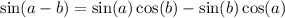
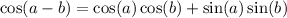
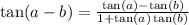
Let's apply the difference identities to all three terms:

`-[\sin(-t)\cos(8\pi)+\cos(-t)\sin(8\pi)]+[\cos(-t)\cos(2\pi)+\sin(-t)\sin(2\pi)]+(\tan(-t)-\tan(5\pi))/(1+\tan(-t)\tan(5\pi))`

We are about to use that cos(even*pi) is 1 and sin(even*pi) is 0 so tan(odd*pi)=0:

Cleaning up the algebra:

`-[\sin(-t)]+[\cos(-t)]+(\tan(-t))/(1)`

Cleaning up more algebra:

`-\sin(-t)+\cos(-t)+\tan(-t)`

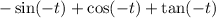
Applying that sine and tangent is odd while cosine is even. That is,

sin(-x)=-sin(x) and tan(-x)=-tan(x) while cos(-x)=cos(x):

`\sin(t)+\cos(t)-\tan(t)`

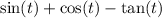
Making the substitution the problem wanted us to:

`a+b-c`

Just for fun you could have wrote c as a/b too since tangent=sine/cosine.