Answer:
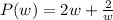
Explanation:
We are given the area of a rectangle is 1 inch square.
You can find the area of a rectangle if you know the dimensions. Let's pretend the dimensions are w and l.
So we given w*l=1.
Now the perimeter of a rectangle with dimensions l and w is 2w+2l.
We want to express P=2w+2l in terms of w only.
We are given that w*l=1 so l=1/w (just divided both sides of w*l=1 by w).
So let's plug it in for l (the 1/w thing).

So
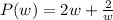 .
.