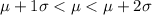Question

The measurement of the height of 600 students of a college is normally distributed with a mean of

175 centimeters and a standard deviation of 5 centimeters.

What percent of students are between 180 centimeters and 185 centimeters in height?

12.5

13.5

34

68

Answer 1

Answer: Second Option

`P(180<X <185)=13.5\%`

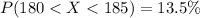
We know that the mean is:

`\mu=175`

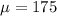
and the standard deviation is:

`\sigma=5`

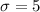
We are looking at the percentage of students between 180 centimeters and 185 centimeters in height.

This is:

`P(180<X <185)`

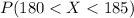
We calculate the Z-score using the formula:

`Z=(X-\mu)/(\sigma)`

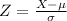
For
`X=180`

`Z_(180)=(180-175)/(5)`

`Z_(180)=1`

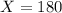
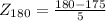
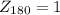
For
`X=185`

`Z_(185)=(185-175)/(5)`

`Z_(185)=2`

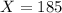
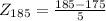
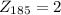
Then we look at the normal table

`P(1<Z<2)`

`P(1<Z<2)=P(Z<2)-P(Z<1)`

`P(1<Z<2)=0.9772-0.8413`

`P(1<Z<2)=0.135`

`P(180<X <185)=13.5\%`

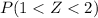
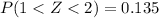
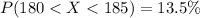
Note: You can get the same conclusion using the empirical rule

Look at the attached image for
`\mu+ 1\sigma <\mu <\mu + 2\sigma`