Question

If g(x) = 2(x − 4), find the value of x if g(x) = 20. (2 points) 32 12 14 10

Answer 1

option c 14

Explanation:

did the test

Answer 2

For this case we have a function of the form
`y = g (x)`

Where:

`g (x) = 2 (x-4)`

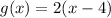
We must find the value of "x" when the function has a value of 20, that is,
`g (x) = 20`:

`2 (x-4) = 20`

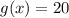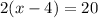
We apply distributive property:

`2x-8 = 20`

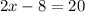
We add 8 to both sides of the equation:

`2x = 20 + 8\\2x = 28`

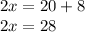
We divide between 2 on both sides of the equation:

`x = \frac {28} {2}\\x = 14`

Answer:

Option C