Question

Browning Labs is testing a new growth inhibitor for a certain type of bacteria. The bacteria naturally grows exponentially each hour at a rate of 6.2%. The researchers know that the inhibitor will make the growth rate of the bacteria less than or equal to its natural growth rate. The sample currently contains 100 bacteria.The container holding the sample can hold only 300 bacteria, after which the sample will no longer grow. However, the researchers are increasing the size of the container at a constant rate allowing the container to hold 100 more bacteria each hour. They would like to determine the possible number of bacteria in the container over time.Create a system of inequalities to model the situation above, and use it to determine how many of the solutions are viable.

Answer 1

Hey! I just answered this on plato. the answer is that it includes negative factors, which makes not all solutions viable.

Answer 2

Look at the attachment

Explanation:

First we need to find out the equations that will represent each inequality:

For the bacteria:

This is an exponential growth equation, the formula is simple:

y≤
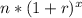`n*(1+r)^(x)` where n is the starting point of the sample, r is the rate and x is the variable dependent on time so:

y≤
`100*(1+0.062)^(x)`

y≤
`100*(1.062)^(x)`

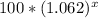
For the container:

This is a line equation, following the formula:

y<mx+b where m is the slope or growing rate (100 more per hour), and b is the starting point (300 bacteria)

y< 100x+300

The graph will be like is showed in the attachment, and the solution is the intersecting area to the right of both functions, since they are trying to find out if the inhibitor works, the rate of growth will be equal or smaller than 6.2% thus closing in to 100 bacterias as a constant in time if it works.