Question

If sine theta equals three over four, what are the values of cos θ and tan θ?

cosine theta equals plus or minus square root of seven over four, tangent theta equals plus or minus two times square root of seven over seven

cosine theta equals plus or minus seven over four, tangent theta equals negative three over seven

cosine theta equals plus or minus square root of seven over 4, tangent theta equals plus or minus three over seven

cosine theta equals plus or minus seven over four, tangent theta equals negative one over seven

Answer 1

Part 1)
`cos(\theta)=(+/-)(√(7))/(4)`

cosine theta equals plus or minus square root of seven over 4

Part 2)
`tan(\theta)=(+/-)(3)/(√(7))`

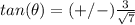
tangent theta equals plus or minus three over square root of seven

or

`tan(\theta)=(+/-)3(√(7))/(7)`

tangent theta equals plus or minus three times square root of seven over seven

Explanation:

we have that

The sine of angle theta is equal to

`sin(\theta)=(3)/(4)`

Is positive

therefore

The angle theta lie on the I Quadrant or in the II Quadrant

Part 1) Find the value of the cosine of angle theta

Remember that

`sin^(2) (\theta)+cos^(2) (\theta)=1`

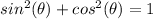
we have

`sin(\theta)=(3)/(4)`

substitute and solve for cosine of angle theta

`((3)/(4))^(2)+cos^(2) (\theta)=1`

`cos^(2) (\theta)=1-((3)/(4))^(2)`

`cos^(2) (\theta)=1-(9)/(16)`

`cos^(2) (\theta)=(7)/(16)`

`cos(\theta)=(+/-)(√(7))/(4)`

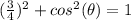
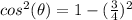
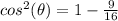
cosine theta equals plus or minus square root of seven over 4

Part 2) Find the value of tangent of angle theta

we know that

`tan(\theta)=(sin(\theta))/(cos(\theta))`

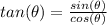
we have

`sin(\theta)=(3)/(4)`

`cos(\theta)=(+/-)(√(7))/(4)`

substitute

`tan(\theta)=((3)/(4))/((+/-)(√(7))/(4))`

`tan(\theta)=(+/-)(3)/(√(7))`

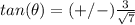
tangent theta equals plus or minus three over square root of seven

Simplify

`tan(\theta)=(+/-)3(√(7))/(7)`

tangent theta equals plus or minus three times square root of seven over seven