Answer:
True.
Explanation:
It is because it is in the form
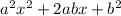 and this equals
and this equals
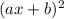 .
.
Why it is in that form: well comparing
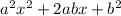 , we have
, we have
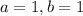 . Testing, plug in those values:
. Testing, plug in those values:
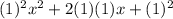
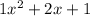
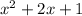 .
.
This has the squared form of
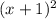 .
.
Test if you like:
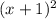
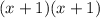
Use foil to expand:
First: x(x)=x^2
Outer: x(1)=x
Inner: 1(x)=x
Last: 1(1)=1
---------------Add together
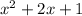
It does indeed equal.