Answer:
![3ab^2\sqrt[3]{b}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1mplgqlk3ws3v8lxdo6bte5jph8zfz4o13.png)
if the problem was
![\sqrt[3]{27a^3b^7}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/cjd85y6hmlcob2c7dgwxhi7l23zwzdxu27.png) .
.
Explanation:
Correct me if I'm wrong by I think you are writing
![\sqrt[3]{27a^3b^7}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/cjd85y6hmlcob2c7dgwxhi7l23zwzdxu27.png) .
.
![\sqrt[3]{27a^3b^7}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/cjd85y6hmlcob2c7dgwxhi7l23zwzdxu27.png)
I'm first going to look at this as 3 separate problems and then put it altogether in the end.
Problem 1:
![\sqrt[3]{27}=(3)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/46qb2fznyke2te2c3kqg8lkf22m228ozwb.png) since
since
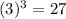 .
.
Problem 2:
![\sqrt[3]{a^3}=(a)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/8y9bogftl51xay3qi1byj6zhyi9tmzrurd.png) since
since

Problem 3:
![\sqrt[3]{b^7}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/v5gtworapm1c57wauic4urvglton5pexi9.png) . This problem is a little harder because
. This problem is a little harder because
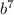 is not a perfect cubes like the others were. But
is not a perfect cubes like the others were. But
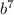 does contain a factor that is a perfect cube. That perfect cube is
does contain a factor that is a perfect cube. That perfect cube is
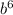 so rewrite
so rewrite
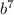 as
as
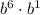 or
or
 .
.
So problem 3 becomes
![\sqrt[3]{b^6 \cdot b}=\sqrt[3]{b^6}\cdot \sqrt[3]{b}=b^2 \cdot \sqrt[3]{b}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4e2syu0wfu6piriypifiby90iuvimwhqwf.png) . The
. The
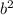 came from this
came from this
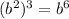 .
.
Anyways let's put it altogether:
![3ab^2\sqrt[3]{b}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1mplgqlk3ws3v8lxdo6bte5jph8zfz4o13.png)