Question

I need to find q, r, s, t
The function is g(x)=2x^2-8

Answer 1

q=0

r=2

s=3

t=-3

Explanation:

q represents the value we should get from evaluating d(-8).

`d(x)=-\sqrt{(1)/(2)x+4}`

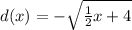
To find d(-8) we use this function here labeled d and replace x with -8:

`d(-8)=-\sqrt{(1)/(2)(-8)+4}`

`d(-8)=-√(-4+4)`

`d(-8)=-√(0)`

`d(-8)=0`

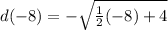
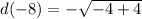
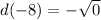
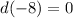
So q is 0 since d(-8)=0.

r represents the value we should get from evaluating f(0).

`f(x)=\sqrt{(1)/(2)x+4}`

To find f(0) we use this function labeled f and repalce x with 0:

`f(0)=\sqrt{(1)/(2)(0)+4}`

`f(0)=√(0+4)`

`f(0)=√(4)`

`f(0)=2`

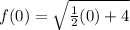
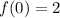
So r is 2 since f(0)=2.

s represents the value we should get from evaluating f(10).

`f(x)=\sqrt{(1)/(2)x+4}`

To find f(10) we use this function labeled f and replace x with 10:

`f(10)=\sqrt{(1)/(2)(10)+4}`

`f(10)=√(5+4)`

`f(10)=√(9)`

`f(10)=3`

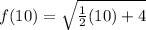
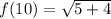
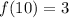
So s is 3 since f(10)=3.

t represents the value we should get from evaluating d(10).

`d(x)=-\sqrt{(1)/(2)x+4}`

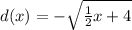
To find d(10) we use the function labeled d and replace x with 10:

`d(10)=-\sqrt{(1)/(2)(10)+4}`

`d(10)=-√(5+4)`

`d(10)=-√(9)`

`d(10)=-3`

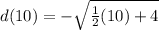
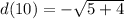
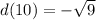
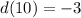
So t is -3 since d(10)=-3

q=0

r=2

s=3

t=-3