Question

Find a vector equation and parametric equations for the line. (Use the parameter t.) The line through the point (0, 11, −8) and parallel to the line x = −1 + 4t, y = 6 − 4t, z = 3 + 6t

Answer 1

The vector equation of the line is
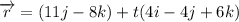`\overrightarrow {r}=(11j-8k)+t(4i-4j+6k)` and parametric equations for the line are
`x=4t`,
`y=11-4t`,
`z=-8+6t`.

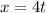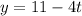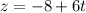Explanation:

It is given that the line passes through the point (0,11,-8) and parallel to the line

`x=-1+4t`

`y=6-4t`

`z=3+6t`

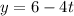
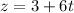
The parametric equation are defined as

`x=x_1+at,y=y_1+bt,z=z_1+ct`

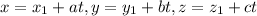
Where, (x₁,y₁,z₁) is point from which line passes through and <a,b,c> is cosine of parallel vector.

From the given parametric equation it is clear that the line passes through the point (-1,6,3) and parallel vector is <4,-4,6>.

The required line is passes through the point (0,11,-8) and parallel vector is <4,-4,6>. So, the parametric equations for the line are

`x=4t`

`y=11-4t`

`z=-8+6t`

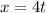
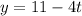
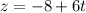
Vector equation of a line is

`\overrightarrow {r}=\overrightarrow {r_0}+t\overrightarrow {v}`

where,
`\overrightarrow {r_0}` is a position vector and
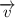`\overrightarrow {v}` is cosine of parallel vector.

`\overrightarrow {r}=(11j-8k)+t(4i-4j+6k)`

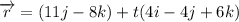
Therefore the vector equation of the line is
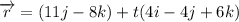`\overrightarrow {r}=(11j-8k)+t(4i-4j+6k)` and parametric equations for the line are
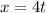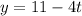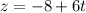`x=4t`,
`y=11-4t`,
`z=-8+6t`.