Question

PLz help

Graph the linear equation. Find three points that solve the equation, then plot then on the graph.
x -3y= -6​

Answer 1

So you will want to graph the following 3 points:

(0,2)

(3,3)

(-3,1)

Then connect the points.

Explanation:

So we have the equation x-3y=-6.

I'm going to solve for y once so I don't have to do it 3 times when choosing a value for x.

x-3y=-6

Subtract x on both sides:

-3y=-x-6

Divide both sides by -3:

`y=(-x)/(-3)+(-6)/(-3)`

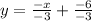
Simplify where you can:

`y=(1)/(3)x+2`

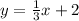
So since this in the slope-intercept form, y=mx+b where slope is m and b is y-intercept we have that (0,2) is on our line. If you plug in 0, you will get 2 like this y=1/3 (0)+2=0+2=2.

Now I'm going to choose easy values to plug in, ones that are divisible by 3 since x is being multiplied by 1/3.

So if x=3, then
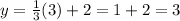`y=(1)/(3)(3)+2=1+2=3`, so (3,3) is on the line.

So if x=-3, then
`y=(1)/(3)(-3)+2=-1+2=1`. so (-3,1) is on the line.

So you will want to graph the following 3 points:

(0,2)

(3,3)

(-3,1)