Question

Two different cars each depreciate to 60% of their respective original values. The first car depreciates at an annual rate of

10%. The second car depreciates at an annual rate of 15%. What is the approximate difference in the ages of the two cars?
A. 1.7 years
B. 2.0 years
C. 3.1 years
D. 5.0 years​

Answer 1

Answer: A) 1.7 Years

Explanation:

Answer 2

A. 1.7 years

Explanation:

Let
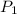`P_1` be the original value of first car,

Since, the car depreciates at an annual rate of 10%,

Let after
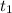`t_1` years the value of car is depreciated to 60%,

That is,

`P_1(1-(10)/(100))^(t_1)=60\%\text{ of }P_1`

`P_1(1-0.1)^(t_1)=0.6P_1`

`0.9^(t_1)=0.6`

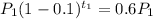
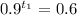
Taking ln on both sides,

`t_1ln(0.9) = ln(0.6)`

`\implies t_1=(ln(0.6))/(ln(0.9))`

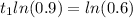
Now, let
`P_2` is the original value of second car,

Since, the car depreciates at an annual rate of 15%

Suppose after
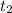`t_2` years it is depreciated to 60%,

`P_2(1-(15)/(100))^(t_2)=60\%\text{ of }P_2`

`P_2(1-0.15)^(t_2)=0.6P_2`

`0.85^(t_2)=0.6`

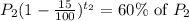
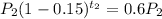
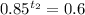
Taking ln on both sides,

`t_2ln(0.85) = ln(0.6)`

`\implies t_2=(ln(0.6))/(ln(0.85))`

`\because t_1-t_2=(ln(0.6))/(ln(0.90))-(ln(0.6))/(ln(0.85))`

`=1.70518303046`

`\approx 1.7`

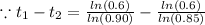
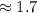
Hence, the approximate difference in the ages of the two cars is 1.7 years,

Option 'A' is correct.