Question

The returns on the common stock of Maynard Cosmetic Specialties are quite cyclical. In a boom economy, the stock is expected to return 22 percent in comparison to 9 percent in a normal economy and a negative 14 percent in a recessionary period. The probability of a recession is 35 percent while the probability of a boom is 10 percent. What is the standard deviation of the returns on this stock?

Answer 1

Answer: 12.51%

Explanation: Probability of normal = 100 - (35+10)=55%

Expected return = Respective return*Respective Probability

= (22*0.1)+(9*0.55)+(-14*0.35) = 2.25%

When

(a) Return = 22% , Probability = 0.1

`\therefore Probability* (Return-Expected Return)^2`

`0.1*(22-2.25)^2=39.006`

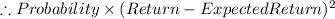
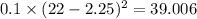
(b) Return = 9%, Probability = 0.55

`\therefore Probability* (Return-Expected Return)^2`

`0.55*(9-2.25)^2=25.05`

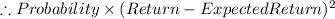
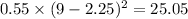
(b) Return = -14%, Probability = 0.35

`\therefore Probability* (Return-Expected Return)^2`

`0.35*(-14-2.25)^2=92.42`

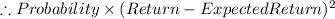
Total=156.48%

`Standard deviation= [Total Probability * (Return-Expected Return)^(2)/ Total probability]^(1/2)`

Standard deviation = 12.51%