Answer:
The first step would to be use quotient rule.
3
Explanation:
ln(x-1)=ln(6)-ln(x)
The first step would to be use quotient rule there on the right hand side:
ln(x-1)=ln(6/x)
*Quotient rule says ln(a/b)=ln(a)-ln(b).
Now that since we have ln(c)=ln(d) then c must equal d, that is c=d.
ln(x-1)=ln(6/x)
implies
x-1=6/x
So you want to shove a 1 underneath the (x-1) and just cross multiply that might be easier.
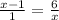
Cross multiplying:
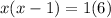
Multiplying/distribute[/tex]
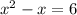
Subtract 6 on both sides:
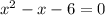
Now this is not too bad to factor since the coefficient of x^2 is 1. All you have to do is find two numbers that multiply to be -6 and add up to be -1.
These numbers are -3 and 2 since -3(2)=-6 and -3+2=-1.
So the factored form of our equation is
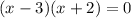
This implies that x-3=0 or x+2=0.
So solving x-3=0 gives us x=3 (just added 3 on both sides).
So solve x+2=0 gives us x=-2 (just subtracted 2 on both sides).
We need to see if these are actually the solutions by plugging them in.
Just a heads up: You can't do log(negative number).
Checking x=3:
ln(3-1)=ln(6)-ln(3)
ln(2)=ln(6/3)
ln(2)=ln(2)
This is true.
Checking x=-2:
ln(-2-1)=ln(6)-ln(-2)
ln(-3)=ln(6)-ln(-2)
We don't need to go further -2 makes the inside of our logarithms negative above.
The only solution is 3.