Explanation:
The formula of a volume of a pyramid:
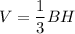
B - base area
H - height
H - height of pyramids
Pyramid A:
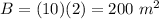
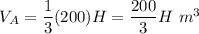
Pyramid B:
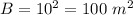
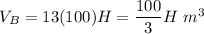
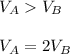
The volume of the pyramid A is twice as large as the volume of the pyramid B.
The new height of pyramid B: 2H
The new volume:
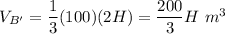
The volume of the pyramid A is equal to the volume of the pyramid B.