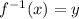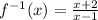Answer:
Part 1)
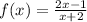 ------->
------->
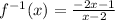
Part 2)
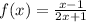 ------->
------->
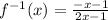
Part 3)
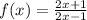 ----->
----->
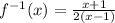
Part 4)
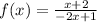 ---->
---->
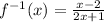
Part 5)
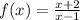 ------->
------->
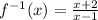
Explanation:
Part 1) we have
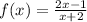
Find the inverse
Let
y=f(x)
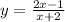
Exchange the variables x for y and t for x
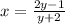
Isolate the variable y
![x=(2y-1)/(y+2)\\ \\ xy+2x=2y-1\\ \\xy-2y=-2x-1\\ \\y[x-2]=-2x-1\\ \\y=(-2x-1)/(x-2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/esj1x40o642iyvwm0xx23sm6llo8d07ay3.png)
Let
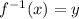
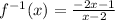
Part 2) we have
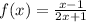
Find the inverse
Let
y=f(x)
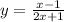
Exchange the variables x for y and t for x
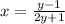
Isolate the variable y
![x=(y-1)/(2y+1)\\ \\2xy+x=y-1\\ \\2xy-y=-x-1\\ \\y[2x-1]=-x-1\\ \\y=(-x-1)/(2x-1)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ck1b6yfuc1irv8l25aw69ec9banxqpqko3.png)
Let
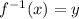
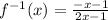
Part 3) we have
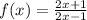
Find the inverse
Let
y=f(x)
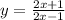
Exchange the variables x for y and t for x
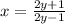
Isolate the variable y
![x=(2y+1)/(2y-1)\\ \\2xy-x=2y+1\\ \\2xy-2y=x+1\\ \\y[2x-2]=x+1\\ \\y=(x+1)/(2(x-1))](https://img.qammunity.org/2020/formulas/mathematics/middle-school/m7h1pr4xu2piwugj91kia8gu1spggbd1jm.png)
Let
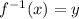
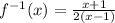
Part 4) we have
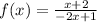
Find the inverse
Let
y=f(x)
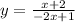
Exchange the variables x for y and t for x
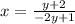
Isolate the variable y
![x=(y+2)/(-2y+1)\\ \\-2xy+x=y+2\\ \\-2xy-y=-x+2\\ \\y[-2x-1]=-x+2\\ \\y=(-x+2)/(-2x-1) \\ \\y=(x-2)/(2x+1)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/vlyu88p3vd8fioa92mecimov2ypukear1g.png)
Let
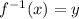
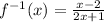
Part 5) we have
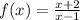
Find the inverse
Let
y=f(x)
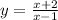
Exchange the variables x for y and t for x
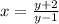
Isolate the variable y
![x=(y+2)/(y-1)\\ \\xy-x=y+2\\ \\xy-y=x+2\\ \\y[x-1]=x+2\\ \\y=(x+2)/(x-1)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/976lnsyhaywf9ky4yee20hskck1q82ir2k.png)
Let