Question

`\frac{x {}^(2) - 4 }{ \sqrt{x {}^(2) - 6x + 9 } } \geqslant 0`
​

Answer 1

First of all, we can observe that

`x^2-6x+9 = (x-3)^2`

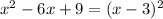
So the expression becomes

`(x^2-4)/(√((x-3)^2)) = (x^2-4)/(|x-3|)`

This means that the expression is defined for every
`x\\eq 3`

Now, since the denominator is always positive (when it exists), the fraction can only be positive if the denominator is also positive: we must ask

`x^2-4 \geq 0 \iff x\leq -2 \lor x\geq 2`

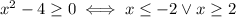
Since we can't accept 3 as an answer, the actual solution set is

`(-\infty,-2] \cup [2,3) \cup (3,\infty)`