Question

The lengths of two sides of a right triangle are 5 inches and 8 inches. What is the difference between the two possible

lengths of the third side of the triangle? Round your answer to the nearest tenth.
O
O
O
O
3.1 inches
3.2 inches
10.0 inches
15.7 inches

Answer 1

B) 3.2 inches

Explanation:

did it on edge

Answer 2

The difference between the two possible lengths of the third side of the triangle is:

3.2 inches

Explanation:

The lengths of two sides of a right triangle are 5 inches and 8 inches.

This means that the third side could be the hypotenuse of the triangle or it could be a leg of a triangle with hypotenuse as: 8 inches.

Let the third side be denoted by c.

• If the third side is the hypotenuse of the triangle.

Then by using the Pythagorean Theorem we have:

`c^2=5^2+8^2\\\\i.e.\\\\c^2=25+64\\\\i.e.\\\\c^2=89\\\\i.e.\\\\c=9.434\ inches`

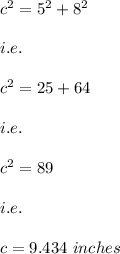
• and if the third side i.e. c is one of the leg of the triangle with hypotenuse 8 inches then the again by using Pythagorean Theorem we have:

`8^2=c^2+5^2\\\\i.e.\\\\64=c^2+25\\\\i.e.\\\\c^2=64-25\\\\i.e.\\\\c^2=39\\\\i.e.\\\\c=√(39)\\\\i.e.\\\\c=6.245\ inches`

Hence, the difference between the two possible lengths of the third side is:

`=9.434-6.245\\\\=3.189\ inches`

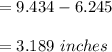
which to the nearest tenth is: 3.2 inches