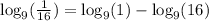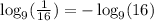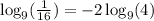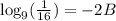Question

Use the properties of logarithms and the values below to find the logarithm indicated.

Answer 1

-2B

Explanation:

log₉ (1/16)

log₉ (16^-1)

log₉ (4^-2)

Using exponent property of logs:

-2 log₉ (4)

Substituting:

-2B

Answer 2

-2B

(I guess this is what you are looking for; didn't need A or C).

Explanation:

It seems like to wants us to to find
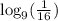`\log_9((1)/(16))` in terms of
`A,B,C`.

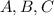First thing I'm going to do is rewrite
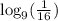`\log_9((1)/(16))` using the quotient rule.

The quotient rule says:

`\log_m((a)/(b))=\log_m(a)-\log_m(b)`

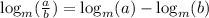
So that means for our expression we have:

`\log_9((1)/(16))=\log_9(1)-\log_9(16)`

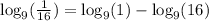
Second thing I'm going to do is say that
`\log_9(1)=0 \text{ since } 9^0=1`.

`\log_9((1)/(16))=\log_9(1)-\log_9(16)`

`\log_9((1)/(16))=-\log_9(16)`

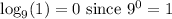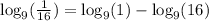
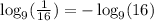
Now I know 16 is 4 squared so the third thing I'm going to do is replace 16 with 4^2 with aim to use power rule.

`\log_9((1)/(16))=\log_9(1)-\log_9(16)`

`\log_9((1)/(16))=-\log_9(16)`

`\log_9((1)/(16))=-\log_9(4^2)`

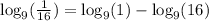
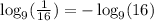
The fourth thing I'm going to is apply the power rule. The power rule say
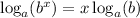`\log_a(b^x)=x\log_a(b)`. So I'm applying that now:

`\log_9((1)/(16))=\log_9(1)-\log_9(16)`

`\log_9((1)/(16))=-\log_9(16)`

`\log_9((1)/(16))=-2\log_9(4)`

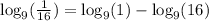
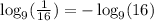
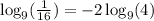
So we are given that
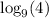`\log_9(4)` is
`B`. So this is the last thing I'm going to do is apply that substitution:

`\log_9((1)/(16))=\log_9(1)-\log_9(16)`

`\log_9((1)/(16))=-\log_9(16)`

`\log_9((1)/(16))=-2\log_9(4)`

`\log_9((1)/(16))=-2B`