Question

A child is twirling a 0.0154-kg ball on a string in a horizontal circle whose radius is 0.149 m. The ball travels once around the circle in 0.639 s. (a) Determine the centripetal force acting on the ball. (b) If the speed is doubled, by what factor does the centripetal force increase?

Answer 1

The answers are: a)Fcp=0,23N b)As Fcp=0,93N, it increases 4 times when the speedis doubled

Step-by-step explanation:

Let´s explain what´s the centripetal force about: It´s the force applied over an object moving on a curvilinear path. This force is directed to the rotation center.

This definition is described this way:

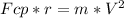`Fcp*r=m*V^2` where:

Fcp is the Centripetal Force

r is the horizontal circle radius

m is the ball mass

V is the tangencial speed, same as the rotation speed

w is the angular speed

Here we need to note that the information we have talks about 1cycle/0,639s (One cycle per 0,639s). We need to express this in terms of radians/seconds. To do it we define that 1cycle is equal to 2pi, so we can find the angular speed this way:

`w=(1cycle/0,639s)*(2pi/1cycle)`

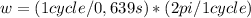
So the angular speed is
`w=9,83rad/s`

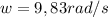
Now that we have this information, we can find the tangencial speed, which will be the relation between the angular speed and the circle radius, this way:

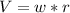`V=w*r` so the tangencial speed is:

`V=(9,83rad/s)*(0,149m)`

`V=1,5m/s`

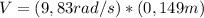
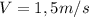
Now we have all the information to find the Centripetal Force:

`Fcp=(m*V^2)/(r)`

`Fcp=((0,0154kg)*(1,5m/s)^2)/(0,149m)`

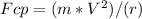
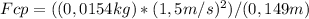
a) So the Centripetal Force is:
`Fcp=0,23N`

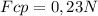
b) If the tangencial speed is doubled, its new value will be 3m/s. replacing this information we will get the new Centripetal Force is:

`Fcp=((0,0154kg)*(3m/s)^2)/(0,149m)`

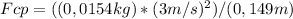
The Centripetal Force is:
`Fcp=0,93N`

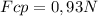
Here we can see that if the speed is doubled, the Centripetal Force will increase four times.