Answer:
0.0837 kJ/K
Step-by-step explanation:
Given:
Temperature of the cold reservoir T,cold = 600 K
Temperature of the hot reservoir T,hot= 1200 K
Heat transferred , Q=100 kJ
Now the entropy change for the cold reservoir
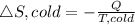

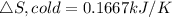
Now the entropy change for the cold reservoir
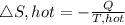
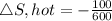
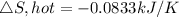
Therefore, the total entropy change for the two reservoir is
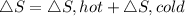
thus,
ΔS=0.1667-0.0833
ΔS=0.0833 kJ/K
Since, the change of entropy is positive thus we can say it is possible and
increase of entropy principle is satisfied