Question

The ages of students in a school are normally distributed with a mean of 16 years and a standard deviation of 1 year. Using the empirical rule, approximately what percent of the students are between 14 and 18 years old?

Answer 1

95% of students are between 14 and 18 years old

Explanation:

First we calculate the Z-scores

We know the mean and the standard deviation.

The mean is:

`\mu=16`

The standard deviation is:

`\sigma=1`

The z-score formula is:

`Z = (x-\mu)/(\sigma)`

For x=14 the Z-score is:

`Z_(14)=(14-16)/(1)=-2`

For x=18 the Z-score is:

`Z_(18)=(18-16)/(1)=2`

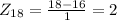
Then we look for the percentage of the data that is between
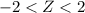`-2 <Z <2` deviations from the mean.

According to the empirical rule 95% of the data is less than 2 standard deviations of the mean. This means that 95% of students are between 14 and 18 years old