Answer:
1) 68%
2) 68%
Explanation:
1) The ages of trees
We know the mean and the standard deviation.
The mean is:
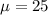
The standard deviation is:
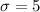
The Z-score formula is:
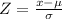
For x=20 the Z-score is:
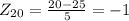
For x=30 the Z-score is:
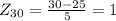
Then we look for the percentage of the data that is between
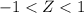 deviations from the mean.
deviations from the mean.
According to the empirical rule 68% of the data is less than 1 standard deviations of the mean. This means that 68% of the trees are between 20 and 30 years old
2) Pizza delivery
First we calculate the Z-scores
We know the mean and the standard deviation.
The mean is:
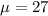
The standard deviation is:
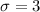
The z-score formula is:
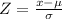
For x=24 the Z-score is:
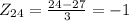
For x=30 the Z-score is:
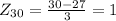
Then we look for the percentage of the data that is between
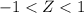 deviations from the mean.
deviations from the mean.
According to the empirical rule 68% of the data is less than 1 standard deviations of the mean. This means that 68% of pizzas are delivered between 24 and 30 minutes