Question

A shaft made of stainless steel has an outside diameter of 42 mm and a wall thickness of 4 mm. Determine the maximum torque T that may be applied to the shaft if the allowable shear stress is equal to 100 MPa.

Answer 1

Step-by-step explanation:

Using equation of pure torsion

`(T)/(I_(polar) )=(t)/(r)`

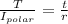
where

T is the applied Torque

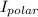`I_(polar)` is polar moment of inertia of the shaft

t is the shear stress at a distance r from the center

r is distance from center

For a shaft with

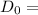`D_(0) =` Outer Diameter

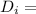`D_(i) =` Inner Diameter

`I_(polar)=(\pi (D_(o) ^(4)-D_(in) ^(4)) )/(32)`

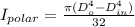
Applying values in the above equation we get

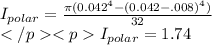`I_(polar) =(\pi(0.042^(4)-(0.042-.008)^(4)))/(32)\\</p><p>I_(polar)= 1.74` x
`10^(-7) m^(4)`

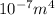
Thus from the equation of torsion we get

`T=(I_(polar) t)/(r)`

Applying values we get

`T=(1.74X10^(-7)X100X10^(6)  )/(.021)`

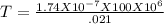
T =829.97Nm