Question

Carbon dioxide at 20°C flows in a pipe at a rate of 0.005 kg/s. Determine the minimum diameter required if the flow is laminar (answer in m).

Answer 1

the required diameter is 0.344 m

Step-by-step explanation:

given data:

flow is laminar

flow of carbon dioxide Q = 0.005 Kg/s

for flow to be laminar, Reynold's number must be less than 2300 for pipe flow and it is given as

`(\rho VD)/(\mu )<2300`

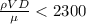
arrange above equation for diameter

\frac{\rho Q D}{\mu A }<2300

dynamic density of carbon dioxide = 1.47×
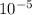`10^(-5)` Pa sec

density of carbon dioxide is 1.83 kg/m³

`(1.83* 0.0056* D)/(1.47* 10^(-5)* (\pi)/(4) * D^(2) )<2300`

`(1.83* 0.0056)/(1.47* 10^(-5)* (\pi)/(4) * 2300)= D`

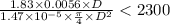
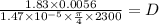
D = 0.344 m