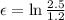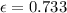Question

A strip ofmetal is originally 1.2m long. Itis stretched in three steps: first to a length of 1.6m, then to 2.2 m, and finally to 2.5 m. Compute the true strain after each step, and the true strain for the entire process (i.e. for stretching from 1.2 m to 2.5 m).

Answer 1

strains for the respective cases are

0.287

0.318

0.127

and for the entire process 0.733

Step-by-step explanation:

The formula for the true strain is given as:

`\epsilon =\ln (l)/(l_(o))`

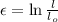
Where

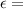`\epsilon =` True strain

l= length of the member after deformation

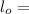`l_(o) =` original length of the member

Now for the first case we have

l= 1.6m

`l_(o) = 1.2m`

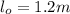
thus,

`\epsilon =\ln (1.6)/(1.2)`

`\epsilon =0.287`

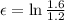
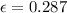
similarly for the second case we have

l= 2.2m

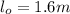`l_(o) = 1.6m` (as the length is changing from 1.6m in this case)

thus,

`\epsilon =\ln (2.2)/(1.6)`

`\epsilon =0.318`

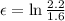
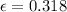
Now for the third case

l= 2.5m

`l_(o) = 2.2m`

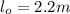
thus,

`\epsilon =\ln (2.5)/(2.2)`

`\epsilon =0.127`

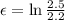
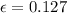
Now the true strain for the entire process

l=2.5m

`l_(o) = 1.2m`

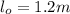
thus,

`\epsilon =\ln (2.5)/(1.2)`

`\epsilon =0.733`