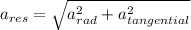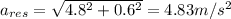Question

A particle moves along a circular path of radius 300 mm. If its angular velocity is θ = (2t) rad/s, where t is in seconds, determine the magnitude of the particle's acceleration when t= 2 s.

Answer 1

4.83m/
`s^(2)`

Step-by-step explanation:

For a particle moving in a circular path the resultant acceleration at any point is the vector sum of radial and the tangential acceleration

Radial acceleration is given by
`a_(radial)=w^(2)`r

Applying values we get
`a_(radial)=(2t)^(2)`X0.3m

Thus
`a_(radial)=1.2t^(2)`

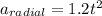
At time = 2seconds
`a_(radial)= 4.8m/s^(2)`

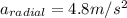
The tangential acceleration is given by
`a_(tangential) =(dV)/(dt)=(d(wr))/(dt)`

`a_(tangential)=(d(2tr))/(dt)`

`a_(tangential)= 2r`

`a_(tangential)=0.6m/s^(2)`

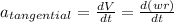
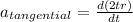
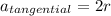
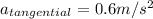
Thus the resultant acceleration is given by

`a_(res) =\sqrt{a_(rad)^(2)+a_(tangential)^(2)}`

`a_(res) =\sqrt{4.8^(2)+0.6^(2)  } =4.83m/s^(2)`