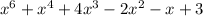Answer:
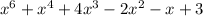
Explanation:
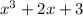
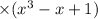
---------------------------------
First step multiply your terms in your first expression just to the 1 in the second expression like so:
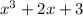
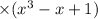
---------------------------------
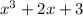 Anything times 1 is that anything.
Anything times 1 is that anything.
That is,
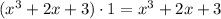 .
.
Now we are going to take the top expression and multiply it to the -x in the second expression.
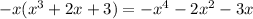 . We are going to put this product right under our previous product.
. We are going to put this product right under our previous product.
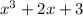
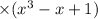
---------------------------------
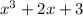
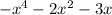
We still have one more multiplication but before we do that I'm going to put some 0 place holders in and get my like terms lined up for the later addition:
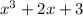
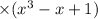
---------------------------------
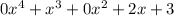
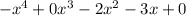
Now for the last multiplication, we are going to take the top expression and multiply it to x^3 giving us
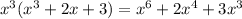 . (I'm going to put this product underneath our other 2 products):
. (I'm going to put this product underneath our other 2 products):
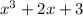
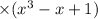
---------------------------------
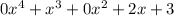
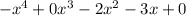
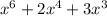
I'm going to again insert some zero placeholders to help me line up my like terms for the addition.
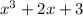
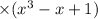
---------------------------------

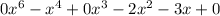
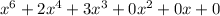
----------------------------------------------------Adding the three products!